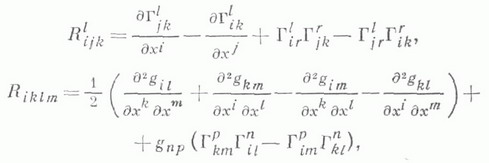КРИВИЗНА

Под большей или меньшей кривизной линии разумеется большее или меньшее уклонение ее от прямолинейного вида, и можно сказать, что окружность тем кривее, чем меньшим радиусом она описана; при очень больших радиусах окружность уклоняется от прямолинейного направления весьма постепенно. Поэтому в математике К. окружности измеряется величиной обратной ее радиусу R; принимают; что К. окружности равна 1/R. К. прочих линий сравнивается с К. окружности следующим образом. К. плоских кривых. Если точка соприкосновения касательной к окружности радиуса R описывает по этой окружности некоторую дугу S, то касательная повертывается при этом на некоторый угол α = S/R. Следовательно, для окружности отношение α/S есть величина постоянная, равная 1/R, то есть К. Отношение α/S угла, составляемого касательными, проведенными в концах дуги S какой-либо кривой, к этой дуге называется средней К. Представим себе, что дуга S кривой уменьшается до совпадения ее концов в одну точку М, тогда отношение α/S стремится к некоторому пределу, который и называется К. в точке М. Окружность, К. которой выражается тем же самым числом как и упомянутый предел, называется кругом К.; радиус ее R — радиусом K. и самая К. кривой в точке М выражается величиной 1/R. Если кривая выражается уравнением f(x,y) = 0, то: 1/R = [d²y/dx²]/[(1 + (dy/dx)²)3/2] = [dx.d²y-dy.d²x]/ds³, где ds = √(dx²+ dy²).

Центр круга К. лежит на нормали точки М и его координаты определяются по формулам X = x — [y'(1 + y'²)]/y " Y = y + (1 + y'²)/y ", где y' = dy/dx; y " = d²y/dx². К.кривых, не умещающихся в плоскости. В кривых таких как винтовая линия, которые описаны в пространстве, первой К. называется тоже предел отношения α/S причем:

Предел положения плоскости, проходящей через точки М и М' кривой и через касательную в точке М, при сближении M' с M назыв. плоскостью соприкосновения. Предел отношения угла, составляемого двумя бесконечно-близкими плоскостями соприкосновения, к соответственной бесконечно малой дуге называется второй К., выражаемой формулой: 1/T = [(d²y.d³z — d²z.d³y)dx + (d²z.d³x — d²x.d³z)dy + (d²x.d³y — d²y.d³x)dz]/[(dy.d²z — dz.d²y)² + (dz.d²x — dx.d²z)² + (dx.d²y — dy.d²z)² ] К. линий, начерченных на поверхности. Эта К. определяется по теореме Менье. Если плоскость соприкосновения в точке M кривой S, начерченной на данной поверхности, составляет угол φ с плоскостью касательной в точке M к поверхности и если R есть радиус К. того нормального сечения, которое имеет с кривой S в точке M общую касательную, то радиус К. кривой S есть R.sinφ. Из всех нормальных сечений, проходящих через какую-либо точку M какой бы то ни было поверхности, существует два, для которых радиус К. достигает максимального или минимального значения — такие два сечения называются главными. Пусть R₁ и R₂ будут радиусы К. главных сечений, проведенных в точке M поверхности, пусть R есть радиус К. одного из промежуточных сечений и пусть α есть угол, составляемый плоскостью этого промежуточного сечения с сечением соответствующим R₁, тогда имеем теорему Эйлера: 1/R = cos²α/R₁ + sin²α/R₂ Если обозначим чрез R' и R " радиусы каких-либо двух перпендикулярных между собой и проходящих через точку М сечений, то: 1/R' + 1/R " = constans. К. 1/R₁ и 1/R₂ главных сечений суть корни квадр. уравнения:

где p=dz/dx; q=dz/dy; r=d²z/dx²; s=d²z/dx.dy; t=d²z/dy². Если деформировать (изгибать) нерастяжимую поверхность, то К. начерченных на ней линий изменяется, но К. проекции такой кривой на касательную плоскость для точки соприкосновения остается неизменной. Лиувилль называет эту К. геодезической. Линия, геодезическая К. которой на всем ее протяжении равна нулю, назыв. геодезической; все плоскости соприкосновения геодезической линии нормальны к поверхности. К. поверхностей. Понятие о К. на поверхности было расширено Гауссом следующим образом: начертим на данной поверхности произвольную замкнутую кривую С, ограничивающую некоторую площадь А; проведем из центра сферы, описанной радиусом, равным единице, прямые, параллельные нормалям поверхности, проведенным в точках кривой С. Эти прямые, выходящие из центра сфера, составят конус, который вырежет на сфере некоторую площадь А', которую Гаусс называет интегральной К. При уменьшении площади А до совпадения всех частей ее в одну точку предел отношения A'/A и назван Гауссом К. поверхности в точке М, в которую обратился контур A. Если R₁ и R₂ радиусы К. главных сечений, то К. поверхности равна 1/R₁R₂. Гаусс доказал при этом теорему: интегральная К. треугольника, образованного тремя геодезическими линиями, равна сумме углов этого криволинейного треугольника за вычетом двух прямых. Смотря по тому, имеют ли R₁ и R₂ одинаковые знаки или противоположные, — К. поверхности будет положительной или отрицательной. Если один из этих радиусов К. R₁ или R₂ обращается в бесконечность, то К. поверхности равна нулю. К. развертывающихся поверхностей во всех точках равна нулю.

        величина, характеризующая отклонение кривой (поверхности) от прямой (плоскости). Отклонение дуги MN кривой L от касательной МР в точке М можно охарактеризовать с помощью т. н. средней кривизны k_cp этой дуги, равной отношению величины ее угла между касательными в точках М и N к длине Δs дуги MN:

        

         Для дуги окружности средняя кривизна равна обратной величине радиуса этой окружности и, т. о., наглядно характеризует степень искривлённости окружности — с уменьшением радиуса увеличивается искривлённость дуги.

         Предельное значение средней кривизны при стремлении точки N кривой к точке М, т. е. при Δs→0, называется кривизной k кривой L в точке М: